Тюрин С.Ф., Алексеев Н.А., Гревцев А.М., Белых А.А.,
г. Пермь
УДК 681.142
МЕТОДИКА АДАПТАЦИИ К ФУНКЦИОНАЛЬНЫМ ОТКАЗАМ
ПОСЛЕДОВАТЕЛЬНОСТНЫХ ЦИФРОВЫХ УЗЛОВ
В отличие от рассматривавшейся
ранее адаптации к отказам комбинационных автоматов [1 – 7] предложен подход
к адаптации последовательностных устройств на основе
адаптации к отказам блока памяти помимо комбинационной части, построенной на
функционально-полных толерантных элементах (ФПТ). Предложена методика такой
адаптации, зависящая от вида отказа блока памяти.
В связи с широким
распространением универсальных программируемых логических устройств (ПЛУ), которые
могут реконфигурироваться в процессе эксплуатации, возникают новые возможности
для построения отказосбоеустойчивых цифровых автоматов. Предлагается сохранять
не исходные логические функции, а базисные функции, позволяющие вычислить исходные
за большее время при заданной модели отказов[1 – 4]. Это позволяет восстановить
вычислительный процесс при некотором снижении производительности. При этом возникает
задача реализации логических функций на массивах элементов с различной разрядностью
слов.
Методика предполагает
специальную декомпозицию исходной системы булевых функций, имеющую особенности
по сравнению с методикой декомпозиции при синтезе автоматов на жесткой логике
– на программируемых логических матрицах (ПЛМ, PLA).
Матричные преобразования функций можно описать выражением PLA( 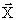 ,A)=
,A)= 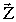 , где
, где 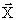 ,
, 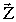 – входной и выходной векторы соответственно, А – начальный адрес массива
данных. Реализация последовательного автомата представляется выражением PLA(
– входной и выходной векторы соответственно, А – начальный адрес массива
данных. Реализация последовательного автомата представляется выражением PLA(
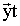 | |
| | 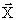 , PAM,A) =
, PAM,A) = 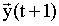 | |
| | 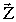 , где
, где 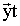 ,
, 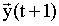 – текущее и последующее состояние автомата, PAM – адрес ячейки памяти
хранения текущего состояния, А – начальный адрес массива данных.
– текущее и последующее состояние автомата, PAM – адрес ячейки памяти
хранения текущего состояния, А – начальный адрес массива данных.
Для вычисления одной булевой функции достаточно задать матрицы Q, D и вектор
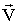 , а для вычисления одной конъюнкции – три вектора
, а для вычисления одной конъюнкции – три вектора 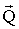 ,
, 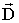 ,
, 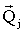 .
.
В случае отказа блока
памяти, количество входных переменных, выходных переменных может
существенно превосходить стандартную разрядность Исследуем методику адаптации
в зависимости от сохранившейся разрядности блока памяти r при различных вариантах
параметров вычисляемых булевых функций.
1. Вычисление многоразрядной конъюнкции.
В этом случае разрядность
входных переменных n > r
Поэтому необходимо анализировать int n/r или μ
подконъюнкций (int
– ближайшее целое число, μ –число
агрегатов, т.е. групп переменных). Для каждой из подконъюнкций
задаются вектора
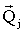 : {
: { 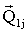 . . .
. . . 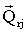 }
}
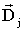 : {
: { 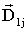 . . .
. . . 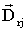 }
}
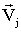 : {
: { 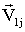 . . .
. . . 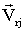 }
}
Так как конъюнкция одна, то вектора 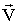 имеют единицы в одних и тех же фиксированных позициях, т.е. по существу
вектор
имеют единицы в одних и тех же фиксированных позициях, т.е. по существу
вектор 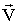 один для всех подконъюнкций.
один для всех подконъюнкций.
Вектора группируются в μ подмассивов с начальными адресами АJ
,j= 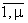 в каждом подмассиве по одному вектору Q, D, V.
в каждом подмассиве по одному вектору Q, D, V.
Процесс вычисления
можно описать следующим образом:
PLA( 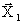 , A1)=V1,
, A1)=V1,
PLA( 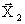 , A2)=V2,
, A2)=V2,
.
.
.
PLA( 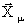 , Aμ)=Vμ,
, Aμ)=Vμ,
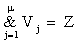 , где Z – результат вычислений. В принципе вычисления заканчиваются при
обнаружении нулевого вектора Vj . В общем виде вычисление
многоразрядной конъюнкции записывается следующим образом:
, где Z – результат вычислений. В принципе вычисления заканчиваются при
обнаружении нулевого вектора Vj . В общем виде вычисление
многоразрядной конъюнкции записывается следующим образом:
PLA( 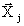 , Aj)=Vj,
, Aj)=Vj,
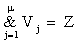 , j = 1, μ (1)
, j = 1, μ (1)
Здесь xj – j–й вектор входных переменных с j-го агрегата, либо с j-й
группы переменных, количество которых превышает r.
2. Вычисление многоразрядной булевой функции.
Пусть булева функция имеет k конъюнкций, причем некоторые из них – многоразрядные
или зависят от переменных, принадлежащих различным узлам. Многоразрядная булева
функция характеризуется параметрами h, k, μ=int h/r, S, где h – разрядность
вектора 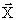 , k – количество многоразрядных конъюнкций (для простоты будем считать,
что все конъюнкции – многоразрядные, остальные можно вычислить отдельно и тривиально),
μ=int h/r – количество подвекторов
, k – количество многоразрядных конъюнкций (для простоты будем считать,
что все конъюнкции – многоразрядные, остальные можно вычислить отдельно и тривиально),
μ=int h/r – количество подвекторов 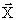 , S – количество подконъюнкций, которое может не совпадать с k* μ
(S ≤ k* μ). Аналогично вычислению многоразрядной конъюнкции задаются
вектора:
, S – количество подконъюнкций, которое может не совпадать с k* μ
(S ≤ k* μ). Аналогично вычислению многоразрядной конъюнкции задаются
вектора:
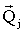 : {
: { 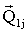 . . .
. . . 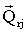 }
}
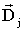 : {
: { 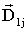 . . .
. . . 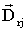 }
}
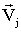 : {
: { 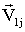 . . .
. . . 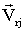 }, j=
}, j= 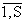 ,
,
которые группируются в μ
массивов с начальными адресами Ai (i=1,
μ).
а) случай k ≤ r. Тогда вектора Vj содержат единицы в позициях, соответствующих
номерам конъюнкций, в которые входит данная подконъюнкция.
В связи с тем, что
индексы вхождения подконъюнкций в конъюнкции на μ
подмассивах не всегда содержат полное множество конъюнкций,
необходимо маскировать биты результатов, соответствующие дополнению индексов
вхождения до полного множества конъюнкций.
Таким образом:
PLA( 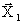 , A1)=V1,
, A1)=V1,
PLA( 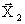 , A2)=V2, (2)
, A2)=V2, (2)
PLA( 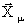 , Aμ)=Vμ,
, Aμ)=Vμ,
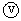 [
[ 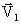 (M/M1) ]
(M/M1) ]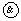 [
[ 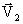 (
(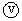 M/M2)
] …. [
M/M2)
] …. [ 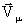 (
(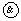 M/Mμ)]=
M/Mμ)]=
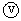
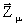
Здесь М - полное множество конъюнкций, где каждой соответствует разряд , Mi
(i= 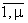 ) – множество индексов вхождений подконъюнкции для i-го входного подвектора
. Причем в массивы Аj в отличии от вычисления одной конъюнкции могут входить
более одного вектора Q, D, V.
) – множество индексов вхождений подконъюнкции для i-го входного подвектора
. Причем в массивы Аj в отличии от вычисления одной конъюнкции могут входить
более одного вектора Q, D, V.
Операции маскирования
можно реализовать в самой процедуре PLA за счет включения
в массивы Aj векторов Q,D,V,
имитирующих включение фиктивной подфункции
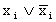 . Вектора, например, имеют вид
. Вектора, например, имеют вид
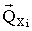 : {0, 0, … 1, 0, … 0}
: {0, 0, … 1, 0, … 0}
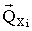 : {0, 0, … 1, 0, … 0}
: {0, 0, … 1, 0, … 0}
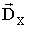 : {0, 0, … 1, 0, … 0}
: {0, 0, … 1, 0, … 0}
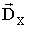 : {0, 0, … 0, 0, … 1}
: {0, 0, … 0, 0, … 1}
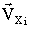 : {1, 0, … 0, 0, … 1}
: {1, 0, … 0, 0, … 1}
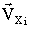 : {1, 0, … 0, 0, … 1}
: {1, 0, … 0, 0, … 1}
Здесь независимо
от значения переменной xi к результатам PLA
добавляются маски, содержащие в первом и последнем битах единицы. Таким образом,
организуется своего рода "смещение" результатов PLA.
Тогда выражение (2) можно записать так:
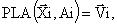
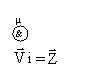 (3)
(3)
Функция равна единице,
если Z≠0. Вектор Z
несет информацию о единичных конъюнкциях исходной функции.
б) случай k>r , т.е. количество конъюнкций больше оставшейся разрядности.
Тогда возможен случай, когда для определения значения некоторых конъюнкций недостаточно
поразрядной конъюнкции (2), (3). Поэтому для идентификации значения конъюнкций
необходимо int k/r векторов разрядностью r и, если некоторая подконъюнкция входит
в конъюнкции, номера которых принадлежат различным векторам идентификации, количество
которых γ, то необходимо γ раз вычислять подконъюнкции с различными
векторами V. Для вычисления многоразрядных конъюнкций в общем случае необходимо
int k/r подмассивов, в каждом из которых необходимы, в свою очередь, подмассивы
по различным входным векторам 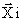 (i=
(i= 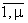 ). Пусть Мк – множество номеров многоразрядных конъюнкций, j=1, int k/r,
Aji – начальный адрес подмассива MAji – множество номеров многоразрядных
конъюнкций соответствующего подмассива. Для вычисления значений конъюнкции необходима
операция пересечения множеств. Ее можно организовать поразрядной конъюнкцией
Vji (результатов) с учетом маскирования битов, соответствующих номерам дополнений
Mk/ MAji (в принципе, Mk- вектор с r единицами).
). Пусть Мк – множество номеров многоразрядных конъюнкций, j=1, int k/r,
Aji – начальный адрес подмассива MAji – множество номеров многоразрядных
конъюнкций соответствующего подмассива. Для вычисления значений конъюнкции необходима
операция пересечения множеств. Ее можно организовать поразрядной конъюнкцией
Vji (результатов) с учетом маскирования битов, соответствующих номерам дополнений
Mk/ MAji (в принципе, Mk- вектор с r единицами).
Маскирование можно организовать либо добавлением в подмассив исходных данных
констант для фиктивной подфункции 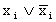 с одинаковым
с одинаковым 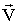 ,
либо непосредственно соответствующей дополнительной командой аналогично 2а.
,
либо непосредственно соответствующей дополнительной командой аналогично 2а.
Процесс вычислений
выглядит следующим образом:
PLA( 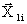 , A1i)=
, A1i)= 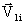 ,
,

.
.
.
PLA( 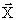 int k/r i, Aint k/r i)=
int k/r i, Aint k/r i)= 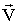 int K/r i , (4)
int K/r i , (4)
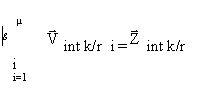
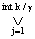 Zj = Z, где (4) учитывает маскирование для псевдопересечения в массивах
Аi.
Zj = Z, где (4) учитывает маскирование для псевдопересечения в массивах
Аi.
В том случае, если
используется отдельная команда, то вычисления имеют вид:
PLA( 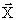 , A11)
, A11)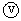 (M1/M11) =
(M1/M11) =
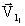
.
.
.
PLA( 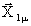 , A1µ)
, A1µ)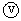 (M1/M1µ) =
(M1/M1µ) =
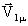
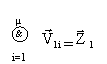
.
.
.
PLA( 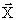 int k/r 1, Aint k/r 1)
int k/r 1, Aint k/r 1)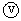 (Mint k/r / Mint k/r 1) =
(Mint k/r / Mint k/r 1) = 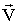 int k/r 1
int k/r 1
PLA( 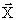 int k/r µ, Aint k/r µ)
int k/r µ, Aint k/r µ)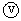 (Mint k/r / Mint k/r µ) =
(Mint k/r / Mint k/r µ) = 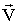 int k/r µ
int k/r µ
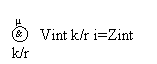
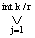 Zj = Z.
Zj = Z.
Вычисления могут заканчиваться при обнаружении нулевого вектора 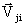
3. Вычисление систем многоразрядных булевых функций (СМБФ)
СМБФ характеризуется
параметрами n, k,µ=int
n/r,
S, m,
где m – количество выходных
функций.
Вычисление системы
функций производится с использованием вариантов 2а, 2б:
а) количество подконъюнкций в СМБФ k ≤ r, n>r, m ≤ r. Используются
выражения (2) или (3)
PLA( 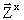 , Az)=
, Az)= 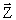
(здесь использовано
выражение (3)).
Аналогично можно
использовать выражение (2)
PLA( 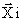 , Ai)=
, Ai)= 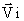 ,
,
 (7)
(7)
PLA( 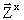 , Az)=
, Az)= 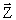 ,
,
где 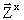 – псевдовыходной вектор, несущий информацию о значениях вычисленных конъюнкций,
Az – массив исходных данных для вычисления по
– псевдовыходной вектор, несущий информацию о значениях вычисленных конъюнкций,
Az – массив исходных данных для вычисления по 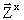 собственно выходного вектора, в котором для каждого разряда
собственно выходного вектора, в котором для каждого разряда 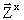 предусмотрен вектор
предусмотрен вектор 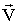 .
.
Следует отметить,
что при задании СМБФ в СНДФ индексы вхождения подконъюнкций
в конъюнкции на различных подвекторах
содержат полное множество многоразрядных
конъюнкций, поэтому необходимость в маскировании дополнения до этого
множества отпадает.
Поэтому процесс вычисления
по выражениям (6), (7) упрощается, что является справедливым и для
вычисления одной функции.
б) Количество подконъюнкций k>r, n>r,m ≤ r.
В этом случае используются выражения (4) и (5).
Псевдовыходной вектор 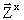 будет иметь разрядность r*int k/r, тогда для получения Z необходимо int
k/r краткое вычисление с последующей дизъюнкцией.
будет иметь разрядность r*int k/r, тогда для получения Z необходимо int
k/r краткое вычисление с последующей дизъюнкцией.
Процесс вычисления имеет вид:
 |
PLA( 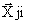 , Aji)=
, Aji)= 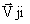 ,
, |
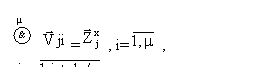 |
PLA( 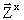 , Azj)=
, Azj)= 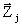 , (8)
, (8) |
| |
int k/r

 =
=

j=1
или


 PLA(
PLA(
 ,
Aji) (Mj/Mij)=
,
Aji) (Mj/Mij)=

PLA(
 ,
Azj)=
,
Azj)=  (9)
(9)
int k/r

 =
=
 ,
i=
,
i=
 ,
, 
j=1
в) n<=r, m>r, k
–любое, т.е. многоразрядным является только выходной сигнал. В этом случае
необходимо int m/r подмассивов
для определения r*int m/r разрядов выходного
вектора, причем входной вектор единственный.
Вычисления имеют
вид:
PLA(  , Ai)=
, Ai)=
 ,
,  (10)
(10)
Для подготовки исходных
данных необходимо провести декомпозицию СМБФ на int m/r подсистем.
г) n>r, k<=r, m>r
В таком случае определяются
значения конъюнкций, количество которых меньше или равно
разрядности r
, т.е. вектор  по выражениям
(6) или (7). Для получения собственно выходных векторов,
количество которых равно int m/r, необходимы вычисления
вида (10). Таким образом, вычисляем по формулам:
по выражениям
(6) или (7). Для получения собственно выходных векторов,
количество которых равно int m/r, необходимы вычисления
вида (10). Таким образом, вычисляем по формулам:
 PLA(
PLA(  , Ai)=
, Ai)=

μ

 =
=  (11)
(11)
i=1
PLA(  , Azj)=
, Azj)=  , i=
, i=  ,
, 
 PLA(
PLA(
 ,
Ai)=
,
Ai)=

μ
 [
[ 
 (M/Mi)]=
(M/Mi)]=  (12)
(12)
i=1
PLA(
 ,
Azj)=
,
Azj)=  , i=
, i=  ,
, 
д) n>r, k>r, m>r
В этом случае после
получения псевдовыходных
векторов  по выражениям
(8) или (9) получают Ε=int m/r собственно выходных
векторов
по выражениям
(8) или (9) получают Ε=int m/r собственно выходных
векторов 

 PLA(
PLA(  ,
Aji) =
,
Aji) = 
PLA(
 ,
AzjE)=
,
AzjE)=  (13)
(13)
int k/r

 =
=
 ,
i=
,
i=
 ,
,
 ,
,

j=1

 PLA(
PLA(  ,
Aji)
,
Aji)  (Mj/Mij)
=
(Mj/Mij)
= 
PLA(
 ,
AzjE)=
,
AzjE)=
 (14)
(14)
int k/r

 =
=
 ,
i=
,
i=
 ,
,
 ,
,

j=1
Предложенная методика
позволяет адаптировать к функциональным
отказам микропрограммные устройства управления,
построенные на основе декомпозиции комбинационного
блока и блока памяти в цепи обратной связи.
Литература
1.
Тюрин
С.Ф. Синтез адаптируемой к отказам цифровой
аппаратуры с резервированием базисных функций
//Приборостроение. – 1999. – № 1. – С.36-39.
2.
Тюрин
С.Ф. Адаптация к отказам одновыходных
схем на генераторах функций с функционально-полными
толерантными элементами //Приборостроение.
– 1999. – № 7. – С.32 – 34.
3.
Тюрин
С.Ф. Проблема сохранения функциональной
полноты булевых функций при «отказах» аргументов
//Автоматика и телемеханика. – 1999. – №
9. – С.176 –186.
4.
Тюрин
С.Ф., Несмелов В.А., Харитонов В.А. и другие.
Программируемое логическое устройство. Патент
РФ № 2146840. Опубл.
БИ № 8, 2000 г.
5.
Тюрин
С.Ф. и другие. Система для программирования
технологическим оборудованием. Патент РФ
№2189623. Опубл.
БИ №26, 2002 г.
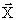 ,A)=
,A)= 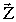 , где
, где 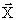 ,
, 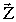 – входной и выходной векторы соответственно, А – начальный адрес массива
данных. Реализация последовательного автомата представляется выражением PLA(
– входной и выходной векторы соответственно, А – начальный адрес массива
данных. Реализация последовательного автомата представляется выражением PLA(
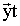 | |
| | 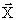 , PAM,A) =
, PAM,A) = 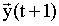 | |
| | 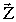 , где
, где 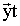 ,
, 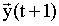 – текущее и последующее состояние автомата, PAM – адрес ячейки памяти
хранения текущего состояния, А – начальный адрес массива данных.
– текущее и последующее состояние автомата, PAM – адрес ячейки памяти
хранения текущего состояния, А – начальный адрес массива данных.
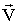 , а для вычисления одной конъюнкции – три вектора
, а для вычисления одной конъюнкции – три вектора 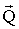 ,
, 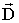 ,
, 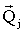 .
.
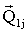 . . .
. . . 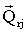 }
}
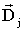 : {
: { 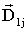 . . .
. . . 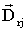 }
}
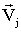 : {
: { 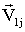 . . .
. . . 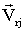 }
}
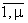 в каждом подмассиве по одному вектору Q, D, V.
в каждом подмассиве по одному вектору Q, D, V.
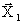 , A1)=V1,
, A1)=V1,
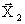 , A2)=V2,
, A2)=V2,
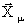 , Aμ)=Vμ,
, Aμ)=Vμ,
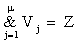 , где Z – результат вычислений. В принципе вычисления заканчиваются при
обнаружении нулевого вектора Vj . В общем виде вычисление
многоразрядной конъюнкции записывается следующим образом:
, где Z – результат вычислений. В принципе вычисления заканчиваются при
обнаружении нулевого вектора Vj . В общем виде вычисление
многоразрядной конъюнкции записывается следующим образом:
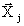 , Aj)=Vj,
, Aj)=Vj,
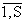 ,
,
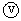 [
[ 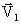 (M/M1) ]
(M/M1) ]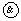 [
[ 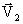 (
(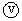 M/M2)
] …. [
M/M2)
] …. [ 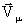 (
(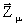
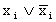 . Вектора, например, имеют вид
. Вектора, например, имеют вид
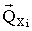 : {0, 0, … 1, 0, … 0}
: {0, 0, … 1, 0, … 0}
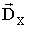 : {0, 0, … 1, 0, … 0}
: {0, 0, … 1, 0, … 0}
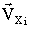 : {1, 0, … 0, 0, … 1}
: {1, 0, … 0, 0, … 1}
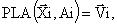
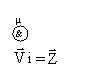 (3)
(3)
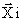 (i=
(i= 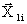 , A1i)=
, A1i)= 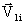 ,
,

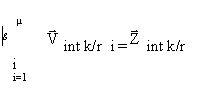
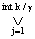 Zj = Z, где (4) учитывает маскирование для псевдопересечения в массивах
Аi.
Zj = Z, где (4) учитывает маскирование для псевдопересечения в массивах
Аi.
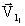
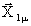 , A1µ)
, A1µ)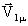
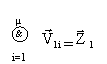
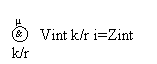
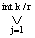 Zj = Z.
Zj = Z.
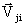
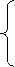
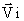 ,
,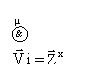 (6)
(6)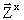 , Az)=
, Az)= 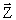
 (7)
(7)
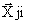 , Aji)=
, Aji)= 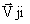 ,
, 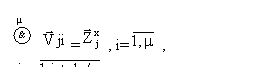
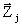 , (8)
, (8) 
 PLA(
PLA(