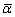 в области
в области 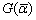 , задаваемой неравенствами типа
, задаваемой неравенствами типа 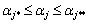 (
( 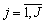 , а само J — число варьируемых параметров;
, а само J — число варьируемых параметров; 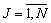 ) и рассчитываемых с помощью ЛПt - сеток [3]. На сегодняшний
день в ПЛП-поиске используются величины J ≤ 51 и N < 220.
) и рассчитываемых с помощью ЛПt - сеток [3]. На сегодняшний
день в ПЛП-поиске используются величины J ≤ 51 и N < 220.
Статников И. Н., Фирсов Г. И.,
г. Москва
УДК 519.240
ПЛАНИРУЕМЫЙ ВЫЧИСЛИТЕЛЬНЫЙ ЭКСПЕРИМЕНТ
В ЗАДАЧАХ МНОГОКРИТЕРИАЛЬНОГО ПРОЕКТИРОВАНИЯ МАШИН И МЕХАНИЗМОВ
В докладе рассматривается применение метода ПЛП-поиска для рационального проведения вычислительных экспериментов на математических моделях (с целью минимизации времени проведения экспериментов при максимально достижимом объеме информации) при анализе и синтезе многопараметрических и многокритериальных динамических систем машин и механизмов.
Общим для проектирования машин и механизмов является то, что они относительно просто поддаются математической формализации как задачи нелинейной (в общем случае) оптимизации: для заданной математической модели требуется подобрать такие значения варьируемых параметров, чтобы они обеспечивали получение экстремальных величин одного или нескольких критериев качества. Значит, приходится иметь дело с задачами многопараметрической и многокритериальной оптимизации.
Среди численных методов поиска оптимальных решений (а именно эти методы в абсолютном большинстве используются для решения практических задач) очевидно не существует универсального, пригодного для решения любой задачи нелинейной оптимизации. Поэтому естественным для разработчиков методов является обращение к вероятностным и статистическим интерпретациям решаемой задачи, в частности, к методу Монте-Карло. Одной из разновидностей этого метода при решении задач проектирования явился ЛП-поиск [1].
Однако при вероятностном и статистическом подходе к решению задачи проектирования возникает важная проблема: обилие информации требует умения ее преобразовывать в характеристики, зависящие и определяющие одновременно свойства проектируемого объекта, а не только отыскивать экстремумы заданных критериев качества. С этой целью в Институте машиноведения РАН был разработан метод ПЛП-поиска (планируемого ЛП-поиска) [2].
Рассмотрим кратко сущность ПЛП-поиска. В основание метода положена рандомизация
расположения векторов 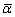 в области
в области 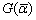 , задаваемой неравенствами типа
, задаваемой неравенствами типа 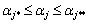 (
( 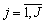 , а само J — число варьируемых параметров;
, а само J — число варьируемых параметров; 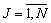 ) и рассчитываемых с помощью ЛПt - сеток [3]. На сегодняшний
день в ПЛП-поиске используются величины J ≤ 51 и N < 220.
) и рассчитываемых с помощью ЛПt - сеток [3]. На сегодняшний
день в ПЛП-поиске используются величины J ≤ 51 и N < 220.
Процесс рандомизации расположения векторов 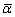 в области
в области 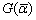 состоит в случайном смешении уровней параметров aijhk
тем или иным способом, где
состоит в случайном смешении уровней параметров aijhk
тем или иным способом, где 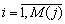 - номер уровня, а M(j) – число уровней варьируемого j-ro
параметра по k - му критерию;
- номер уровня, а M(j) – число уровней варьируемого j-ro
параметра по k - му критерию; 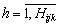 , а Hijk – число значений k - го критерия
, а Hijk – число значений k - го критерия
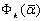 на i - м уровне j-го параметра;
на i - м уровне j-го параметра; 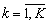 - номер критерия, где К -количество критериев качества. В результате
обработки всех N вычислительных экспериментов, проведенных на математической
модели, появляются выборочные множества значений
- номер критерия, где К -количество критериев качества. В результате
обработки всех N вычислительных экспериментов, проведенных на математической
модели, появляются выборочные множества значений 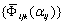 , где
, где 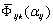 – среднее значение k-го критерия качеств в i-м сечении
j-го варьируемого параметра. Естественно рассматривать множество значений
– среднее значение k-го критерия качеств в i-м сечении
j-го варьируемого параметра. Естественно рассматривать множество значений
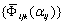 как аналог чувствительности в среднем критерия
как аналог чувствительности в среднем критерия 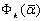 к изменениям параметра aj при возможных сочетаниях
значений других варьируемых параметров в заданной области
к изменениям параметра aj при возможных сочетаниях
значений других варьируемых параметров в заданной области 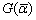 .
.
Анализ графических зависимостей 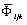 от aij позволяет визуально (конечно, приближенно) выделять
области
от aij позволяет визуально (конечно, приближенно) выделять
области 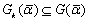 , концентрированно содержащие наилучшие результаты по
, концентрированно содержащие наилучшие результаты по 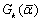 , и одновременно, область
, и одновременно, область 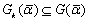 , в которой сконцентрировано множество Парето-решений, либо компромиссных
решений, если задана какая-либо схема компромисса. Разумеется, такой анализ
подается и автоматизации, что требует дополнительной программной реализации.
, в которой сконцентрировано множество Парето-решений, либо компромиссных
решений, если задана какая-либо схема компромисса. Разумеется, такой анализ
подается и автоматизации, что требует дополнительной программной реализации.
На сегодняшний день все алгоритмы ПЛП-поиска реализованы в среде MATLAB [4]. Структура разработанного пакета включает следующие основные этапы:
1) определение существенных параметров am (m ≤
J) в смысле их влияния на значения каждого критерия 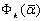 ;
;
2) выделение областей концентрации 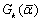 наилучших решений по каждому критерию
наилучших решений по каждому критерию 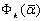 при заданной метрике
при заданной метрике 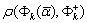 , где
, где 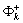 — экстремальное значение k-го критерия качества, заранее известное
или определяемое по ходу проведения вычислительных экспериментов;
— экстремальное значение k-го критерия качества, заранее известное
или определяемое по ходу проведения вычислительных экспериментов;
3) построение на основе определенных существенных параметров и выделенных
подобластей регрессионных зависимостей 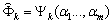 ;
;
4) выделение в K-мерном пространстве критериев множества с высокой
концентрацией точек Парето (или, если возможно, построение поверхности Парето);
в случае задания какой-либо схемы компромисса – выделение подобласти 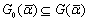 , содержащей наибольшую концентрацию требуемых компромиссных решений.
, содержащей наибольшую концентрацию требуемых компромиссных решений.
Наличие графических зависимостей 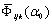 , а также возможность определения влияющих параметров на критерии качества
[2] с требуемой доверительной вероятностью, в значительной мере решают проблему
интегрирования огромной численной информации, полученной в эксперименте, в ясные
и поддающиеся логическому анализу (вплоть до "здравого смысла") характеристики.
, а также возможность определения влияющих параметров на критерии качества
[2] с требуемой доверительной вероятностью, в значительной мере решают проблему
интегрирования огромной численной информации, полученной в эксперименте, в ясные
и поддающиеся логическому анализу (вплоть до "здравого смысла") характеристики.
Таким образом, метод ПЛП-поиска не только позволяет на основе проведения имитационных модельных экспериментов осуществить квазиравномерный просмотр. При этом путем построения аппроксимационных моделей критериев в зависимости от варьируемых параметров оказывается возможным провести оценку чувствительности критериев в среднем по этим параметрам
Изложенный подход применялся при решении целого ряда конкретных задач исследования, оптимизации и идентификации различных механических систем, в частности для синтеза шарнирно-рычажного четырехзвенного механизма съемного гребня чесальной машины с разгружателем и проектирования зубчато-рычажного механизма с остановкой, широко используемого в эмалировочных автоматах, в автоматах пищевой и полиграфической промышленности, в револьверных подачах прессов и т.д. С помощью рандомизации области изменения параметров выполнены оптимизация резонансного преобразователя для судовых валопроводов, используемого в целях снижения уровня их продольных колебаний, и получены оптимальные значения инерционно-жесткостных параметров динамической системы с 23 степенями свободы, описывающей двухступенчатый планетарный судовой редуктор. Показана принципиальная возможность отстройки собственных частот от заданных рабочих диапазонов для конкретных моделей редукторов.
Подведем некоторые итоги. Доказывая эффективность ПЛП-поиска по сравнению со “слепым” способом поиска экстремумов, не предлагается отбрасывать последний. Однако, очевидно, что ПЛП-поиск не только может помогать скорейшему поиску экстремумов, если это требуется, но и дает информацию о влиятельности варьируемых параметров и, что также важно, способствует возникновению вопросов, связанных с исследованием пространства варьируемых параметров (в частности, результаты ПЛП-поиска могут помочь выбрать эффективную схему компромисса).
Литература