Дударь Е. С.,
г. Пермь
УДК 622.4
РАСЧЕТ ГИДРАВЛИЧЕСКИХ СЕТЕЙ МЕТОДОМ КОНЕЧНЫХ
ЭЛЕМЕНТОВ
Описано
применение метода конечных элементов (МКЭ) для расчета гидравлических сетей
произвольной сложности с любым режимом движения жидкости в ветвях. Разработана
компьютерная программа, позволяющая учитывать работу источников энергии, влияние
местных сопротивлений и шероховатости поверхности.
Метод конечных элементов широко используется
как для решения задач механики сплошной среды, так и для анализа дискретных
систем, состоящих из конечного числа связанных элементов. Пример расчета гидравлической
сети с ламинарным движением жидкости приведен в [1]. В предложенной работе
рассмотрено применение метода для расчета сети с любым режимом движения жидкости
в отдельных ветвях.
В соответствии с МКЭ сеть разбивается на отдельные элементы (ветви). Для задания
топологии сети каждому элементу ставится в соответствие упорядоченная пара узлов
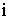 и
и 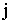 , положительным направлением считается направление от узла
, положительным направлением считается направление от узла 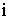 к узлу
к узлу 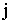 . Искомыми величинами являются давления в узлах сети. Элементы сети делятся
на активные и пассивные. К активным элементам относятся вентиляционные установки,
к пассивным – элементы, не содержащие вентиляторов. Для получения системы уравнений
относительно искомых давлений устанавливается зависимость между узловыми давлениями
и объемным расходом жидкости в элементе сети.
. Искомыми величинами являются давления в узлах сети. Элементы сети делятся
на активные и пассивные. К активным элементам относятся вентиляционные установки,
к пассивным – элементы, не содержащие вентиляторов. Для получения системы уравнений
относительно искомых давлений устанавливается зависимость между узловыми давлениями
и объемным расходом жидкости в элементе сети.
В случае ламинарного течения жидкости искомая зависимость 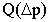 определяется из закона Пуазейля [3] и является линейной. Для турбулентного
режима течения жидкости в трубе связь между расходом и перепадом давления устанавливается
законом Дарси [3] и является нелинейной. Уравнение Дарси, записанное в безразмерном
виде
определяется из закона Пуазейля [3] и является линейной. Для турбулентного
режима течения жидкости в трубе связь между расходом и перепадом давления устанавливается
законом Дарси [3] и является нелинейной. Уравнение Дарси, записанное в безразмерном
виде 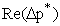 , справедливо для труб любых геометрических размеров и для жидкостей
с любыми свойствами. Зависимость
, справедливо для труб любых геометрических размеров и для жидкостей
с любыми свойствами. Зависимость 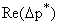 можно представить в виде графика универсальной кривой для ряда значений
относительной шероховатости, при построении которого использованы данные опытов
Никурадзе [3].
можно представить в виде графика универсальной кривой для ряда значений
относительной шероховатости, при построении которого использованы данные опытов
Никурадзе [3].
Характеристика активного элемента сети является заданной величиной. При использовании
МКЭ характеристика вентилятора рассматривается в виде зависимости 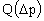 , при этом положительное значение расхода соответствует движению воздуха
от всасывающего отверстия к диффузору, а положительный перепад давления – есть
разница давлений между диффузором и всасывающим отверстием вентилятора. При
прямой установке вентилятора поток направлен от узла
, при этом положительное значение расхода соответствует движению воздуха
от всасывающего отверстия к диффузору, а положительный перепад давления – есть
разница давлений между диффузором и всасывающим отверстием вентилятора. При
прямой установке вентилятора поток направлен от узла 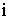 к узлу
к узлу 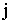 , при этом расход будет положительной величиной, а перепад давления –
отрицательной. При обратной установке вентилятора знаки расхода и перепада давления
соответственно поменяются. В обоих случаях характеристика активного элемента
сети является восходящей. Известно, что такой вид кривой
, при этом расход будет положительной величиной, а перепад давления –
отрицательной. При обратной установке вентилятора знаки расхода и перепада давления
соответственно поменяются. В обоих случаях характеристика активного элемента
сети является восходящей. Известно, что такой вид кривой 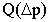 соответствует устойчивой работе вентилятора [2] и одновременно обеспечивает
сходимость итерационной процедуры численного решения системы нелинейных алгебраических
уравнений[4].
соответствует устойчивой работе вентилятора [2] и одновременно обеспечивает
сходимость итерационной процедуры численного решения системы нелинейных алгебраических
уравнений[4].
Выполняя операцию суммирования по всем элементам, получают систему нелинейных
алгебраических уравнений, для решения которой используется метод простой итерации.
На первой итерации течение в каждой ветви принято ламинарным.
Из закона сохранения массы следует, что для вектора
расходов ненулевыми будут только те компоненты, которые соответствуют граничным
узлам с заданным расходом. В тех граничных узлах, где расход не задан, должно
быть задано давление. В одном граничном узле давление задается обязательно,
так как оно определяется с точностью до константы.
Данный метод был
применен для расчета вентиляционной сети калийного рудника, содержащего 285
ветвей и 219 узлов. Для получения решения с точностью 0,5% по узловым давлениям
потребовалось 9 итераций.
Литература
- Норри Д., Фриз Ж. де. Введение в метод конечных элементов. – М.: Мир,198.
– 304 с.
- Меренков А.П., Хасилев В.Я. Теория гидравлических цепей. – М.: Наука,1985.
– 278 с.
- Шлихтинг Г. Теория пограничного слоя. – М.: Наука,1974. – 712 с.
- Галлагер Р. Метод конечных элементов. Основы. – М.: Мир, 1984. – 428 с.
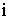 и
и 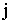 , положительным направлением считается направление от узла
, положительным направлением считается направление от узла 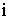 к узлу
к узлу 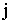 . Искомыми величинами являются давления в узлах сети. Элементы сети делятся
на активные и пассивные. К активным элементам относятся вентиляционные установки,
к пассивным – элементы, не содержащие вентиляторов. Для получения системы уравнений
относительно искомых давлений устанавливается зависимость между узловыми давлениями
и объемным расходом жидкости в элементе сети.
. Искомыми величинами являются давления в узлах сети. Элементы сети делятся
на активные и пассивные. К активным элементам относятся вентиляционные установки,
к пассивным – элементы, не содержащие вентиляторов. Для получения системы уравнений
относительно искомых давлений устанавливается зависимость между узловыми давлениями
и объемным расходом жидкости в элементе сети.
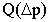 определяется из закона Пуазейля [3] и является линейной. Для турбулентного
режима течения жидкости в трубе связь между расходом и перепадом давления устанавливается
законом Дарси [3] и является нелинейной. Уравнение Дарси, записанное в безразмерном
виде
определяется из закона Пуазейля [3] и является линейной. Для турбулентного
режима течения жидкости в трубе связь между расходом и перепадом давления устанавливается
законом Дарси [3] и является нелинейной. Уравнение Дарси, записанное в безразмерном
виде 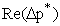 , справедливо для труб любых геометрических размеров и для жидкостей
с любыми свойствами. Зависимость
, справедливо для труб любых геометрических размеров и для жидкостей
с любыми свойствами. Зависимость 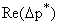 можно представить в виде графика универсальной кривой для ряда значений
относительной шероховатости, при построении которого использованы данные опытов
Никурадзе [3].
можно представить в виде графика универсальной кривой для ряда значений
относительной шероховатости, при построении которого использованы данные опытов
Никурадзе [3].
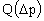 , при этом положительное значение расхода соответствует движению воздуха
от всасывающего отверстия к диффузору, а положительный перепад давления – есть
разница давлений между диффузором и всасывающим отверстием вентилятора. При
прямой установке вентилятора поток направлен от узла
, при этом положительное значение расхода соответствует движению воздуха
от всасывающего отверстия к диффузору, а положительный перепад давления – есть
разница давлений между диффузором и всасывающим отверстием вентилятора. При
прямой установке вентилятора поток направлен от узла