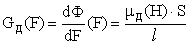, (1)
Афанасьев С. Н., Середа Ю. А.,
г. Пермь
УДК 681.142
Математическая модель процесса перемагничивания
параллельных магнитных цепей
На базе не используемого ранее в технике эффекта разработаны основы теории поочередного перемагничивания параллельных магнитных цепей, состоящие из обобщенной математической модели процесса перемагничивания и аналитических соотношений для инженерного анализа и синтеза преобразователей электроэнергии с повышенным КПД.
Впервые физическое и математическое описание эффекта поочередного перемагничивания параллельных магнитных цепей совместно с основными схемными решениями инверторов было приведено в депонированной рукописи в 1986 году [1].
Разработанная модель [2] позволяет рассчитать процессы перемагничивания отдельных замкнутых разнородных магнитопроводов, параллельных относительно общей намагничивающей ЭДС или МДС, или в другом варианте – процесс перемагничивания замкнутых концентрических слоев одного сплошного магнитопровода, отличающихся величиной вихревых токов.
Первый вариант позволяет за счет использования эффекта поочередного перемагничивания параллельных магнитопрововдов организовать автоматическое регулирование процесса перемагничивания сердечников трансформаторов по предельному магнитному циклу без скачков намагничивающего тока. Это дает возможность создавать трансформаторы высокочастотных преобразователей напряжения (инверторов) на большую мощность, с высоким КПД и незначительными габаритами. Такие инверторы являются базой сварочных аппаратов, установок для индукционного разогрева металлов и др. [3; 4].
Второй вариант позволяет рассчитать вихревые токи и потери энергии в сплошном магнитопроводе, в листовом магнитопроводе и в отдельных частицах ферритового магнитопровода. В последних двух случаях, используя скачок общей МДС, можно рассчитать и получить полный анализ той части магнитной «вязкости» материала, которая вызвана вихревыми токами [2].
Математическое моделирование проводилось с учетом следующих исходных данных:
При моделировании использовался единый нелинейный магнитный параметр – динамическая магнитная проводимость цепи GД (F):
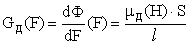, (1)
где F=Hl – текущая намагничивающая МДС магнитопровода;
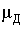– дифференциальная магнитная проницаемость материала цепи;
S, l – средние площадь и длина сердечника;
Ф – магнитный поток цепи.
В этом случае для ЭДС самоиндукции и взаимоиндукции можно записать:
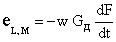(2)
где w – число витков обмотки, размещенной на рассматриваемом сердечнике.
При программировании нелинейные зависимости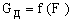 
для каждого сердечника могут быть заданы графически, аналитически или
табличным способом, но с учетом перемагничивания материала по полным и частым
циклам петли гистерезиса.
Обобщенная математическая модель составлялась для n параллельных магнитных
цепей, охваченных m обмотками. Первичная обмотка w1 охватывает все
n сердечников. Вторичные обмотки охватывают каждая свое число сердечников и
подключены каждая к своей нагрузке. Магнитные проводимости всех цепей рассеяния
обмоток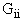 
и взаимоиндукции между ними 
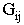известны.
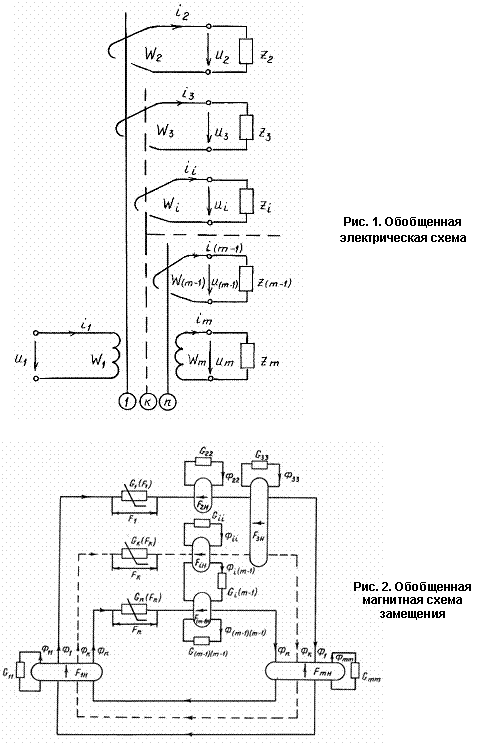
Обобщенная электрическая схема представлена на рис. 1, а соответствующая ей обобщенная магнитная схема замещения на рис. 2.
В этом случае связь между известным первичным и вторичными напряжениями может быть установлена следующим уравнением:
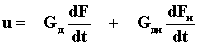, (3)
где: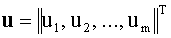 
– вектор напряжений на обмотках;
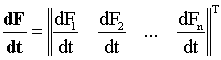- вектор производственных намагничивающих МДС сердечников;
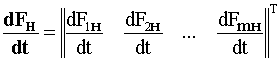– вектор производных МДС обмоток;
- матрица динамически магнитных проводимостей сердечников;
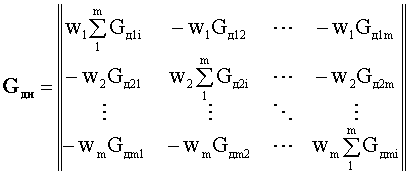- матрица динамических проводимостей магнитных цепей.
Таким образом, матрицы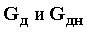 
математически полностью описывают параллельные магнитные цепи, состоящие
в общем случае из n нелинейных магнитных сердечников, на которых различным образом
размещено m обмоток.
Вектора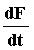 
и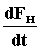 
на каждом шаге интегрирования вычисляются с помощью векторов МДС:
 |
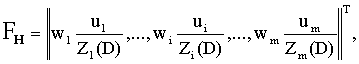(4) |
 |
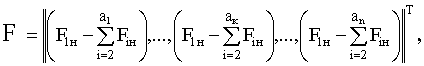где FH – вектор МДС обмоток;
F – вектор намагничивающих МДС сердечников;
Zi (D) – интегро-дифференциальный оператор над Fiн ;
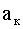– число вторичных обмоток на к-том сердечнике.
В случае, когда все цепи нагрузки являются чисто активными или активно-индуктивными,
система уравнений для вычисления векторов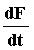
и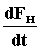
будет иметь вид:
 |
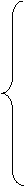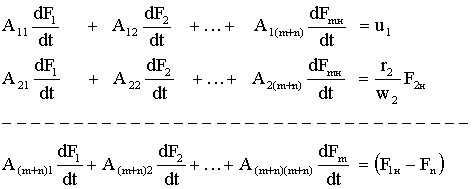(5) |
где: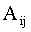 
– нелинейные коэффициенты, зависящие от текущих МДС.
На рис. 3 представлена схема трансформатора с датчиком насыщения 2 и обмотками
датчика w3 , w4.
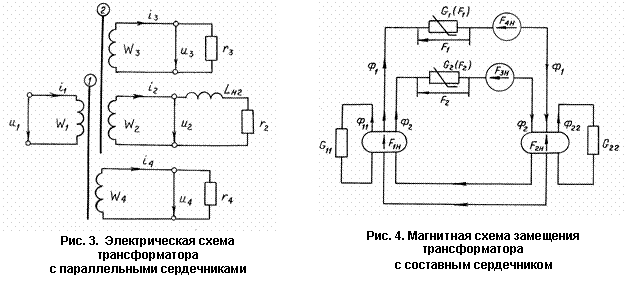
При пренебрежении магнитными цепями взаимоиндукции между обмотками и рассеяния слаботочных обмоток датчика w3 и w4 можно составить магнитную схему замещения (рис.4).
Текущие напряжения трансформатора:
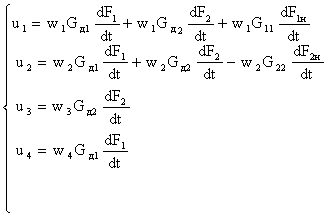(6)
Для вычисления на каждом шаге интегрирования переменных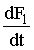 
, 
, 
, 
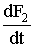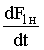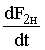используются уравнения МДС:
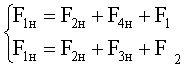, (7)
которые после подставок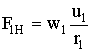 
, 
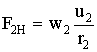и с учетом уравнений 6, содержащих магнитные проводимости рассеяния,
получают вид:
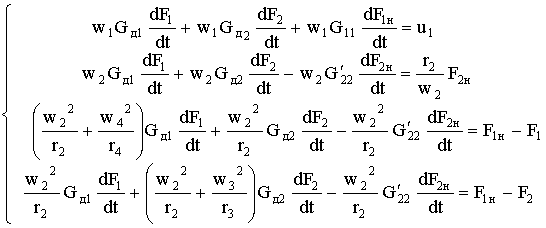, (8)
где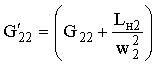 
– расчетная магнитная проводимость рассеяния второй обмотки.
При заданном входном воздействии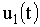 
для переменных 
, 
, 
, 
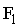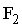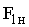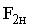всегда можно определить начальные значения, а дальше их вычислять после
каждого шага интегрирования.
Полученные авторами 13 авторских свидетельств (А.С.), патентов, положительных решений на выдачу патента:
Проведенные эксперименты [2; 5], полностью подтверждают достоверность обобщенной математической модели, высокие эксплуатационные параметры предлагаемых высокочастотных трансформаторов и возможность их реализации на предприятиях г. Перми и Пермской области.
Литература